How Union and Set Intersection are Used in Data Analysis

Data analysis is based on operations on sets. The simplest of these are intersection and union. Let's repeat what these operations are and what properties they have.

Intersection of Sets

The intersection A ∩ B of two sets A and B consists of elements that belong to both original sets.

Only those elements that are in both A and B at the same time will get into the intersection.

The intersection of two sets is also a set. If there are no elements that belong to both sets at once, then the intersection of the sets will be empty: A ∩ B = ∅.

Set Intersection Examples

If H is the set of exercises for arms and L is the set of exercises for legs, then H ∩ L is the set of exercises that for arms and legs.
If A is a set of apples and G is a set of green objects, then A ∩ G is a set of green apples.
If E is the set of English songs and J is the set of Jennifer Lopez songs, then E ∩ J is the set of Jennifer Lopez songs in English.

‍

Union of Sets

The union A ∪ B consists of all elements of the original sets A and B together. That is, all elements that were in at least one of the original sets will fall into the union.

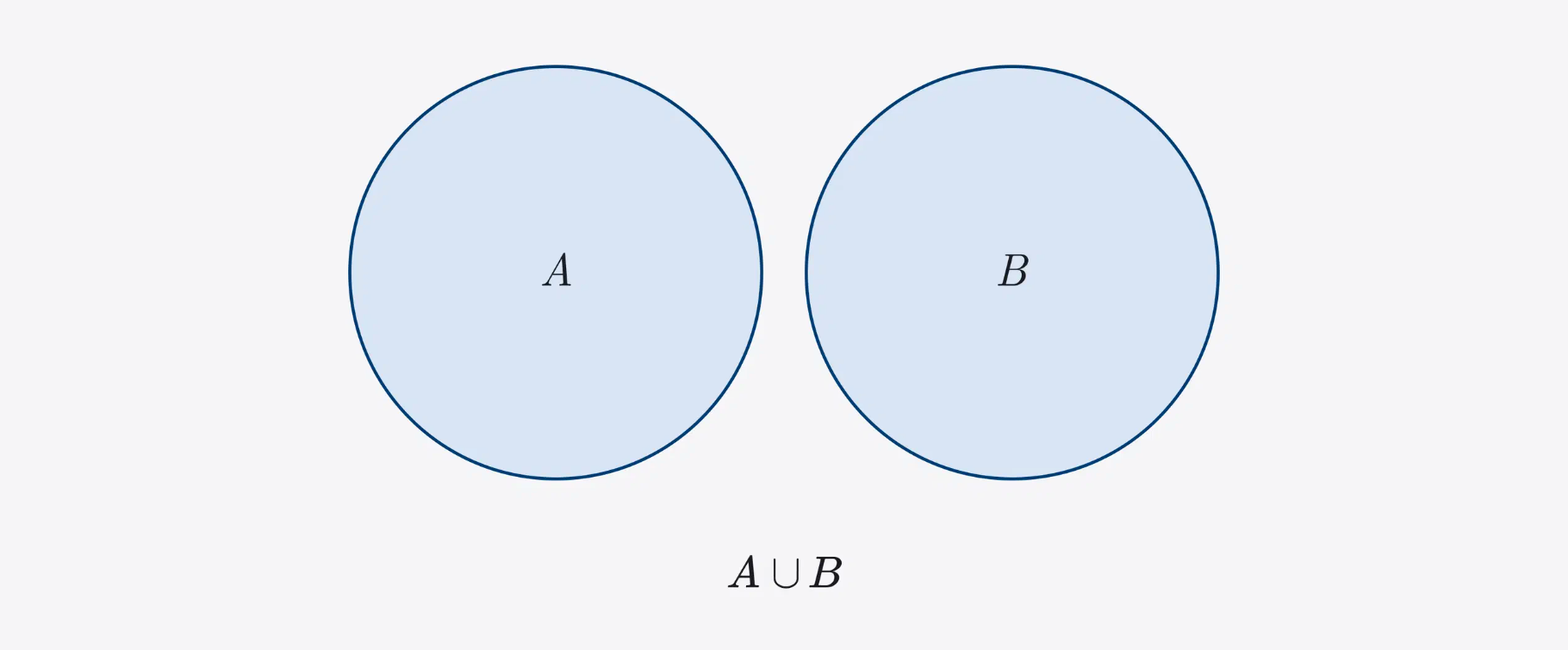
All elements of the union are either in set A or in set B.

The union includes all the elements that were found in the sets individually, but only once. If A = {100, 200, 300, 400, 500}, B = {100, 500, 1000, 1500}, then A ∪ B = {100, 200, 300, 400, 500, 1000, 1500}.

Union of Sets Examples

If B is a set of books on healthy eating and A is a set of articles on healthy eating, then B ∪ A is a set of books and articles on healthy eating.
If X is the set of oranges and Y is the set of tangerines, then X ∪ Y is the total set of oranges and tangerines together.
If F is the set of grades from one to five and L is the set of grades from three to six, then F ∪ L is the set of grades from one to six.

This is how the options for the mutual arrangement of sets look when intersected.

With three sets, everything is the same: the union A ∪ B ∪ C will contain the interior of all three circles.

‍

Intersection and Union of Sets in Data Analysis

A dataset is a set. The intersection and union operations are the most basic of the possible data operations. For example, let's take two sets: the first - customers who called the call center, the second - customers who texted in the chat. Finding customers who both called the call center and wrote to the chat is an intersection. Gathering a data base of customers who contacted through any of these channels is a union.

The intersection and union operators are used in all programming languages. Including those that are most often used by analysts. For example, in SQL, the set intersection operation corresponds to the INTERSECT operator, and the union operation to the UNION operator. In Python, these operations are called intersection and union.

SQL also uses the JOIN operator to join tables, but it has different properties. The set union operator is exactly the same as UNION: this operator joins tables, but leaves only unique values.

What about properties? Commutativity, associativity, distributivity - these properties of operations on sets are also used in programming languages. When an analyst understands how sets interact, they can solve their workloads faster and make fewer mistakes.

‍

Intersection and Union Properties of Sets

Operations on sets, like operations on numbers, have a number of properties. Intersection can be related to multiplication, and union to addition. Then you get the properties familiar to you from middle school!

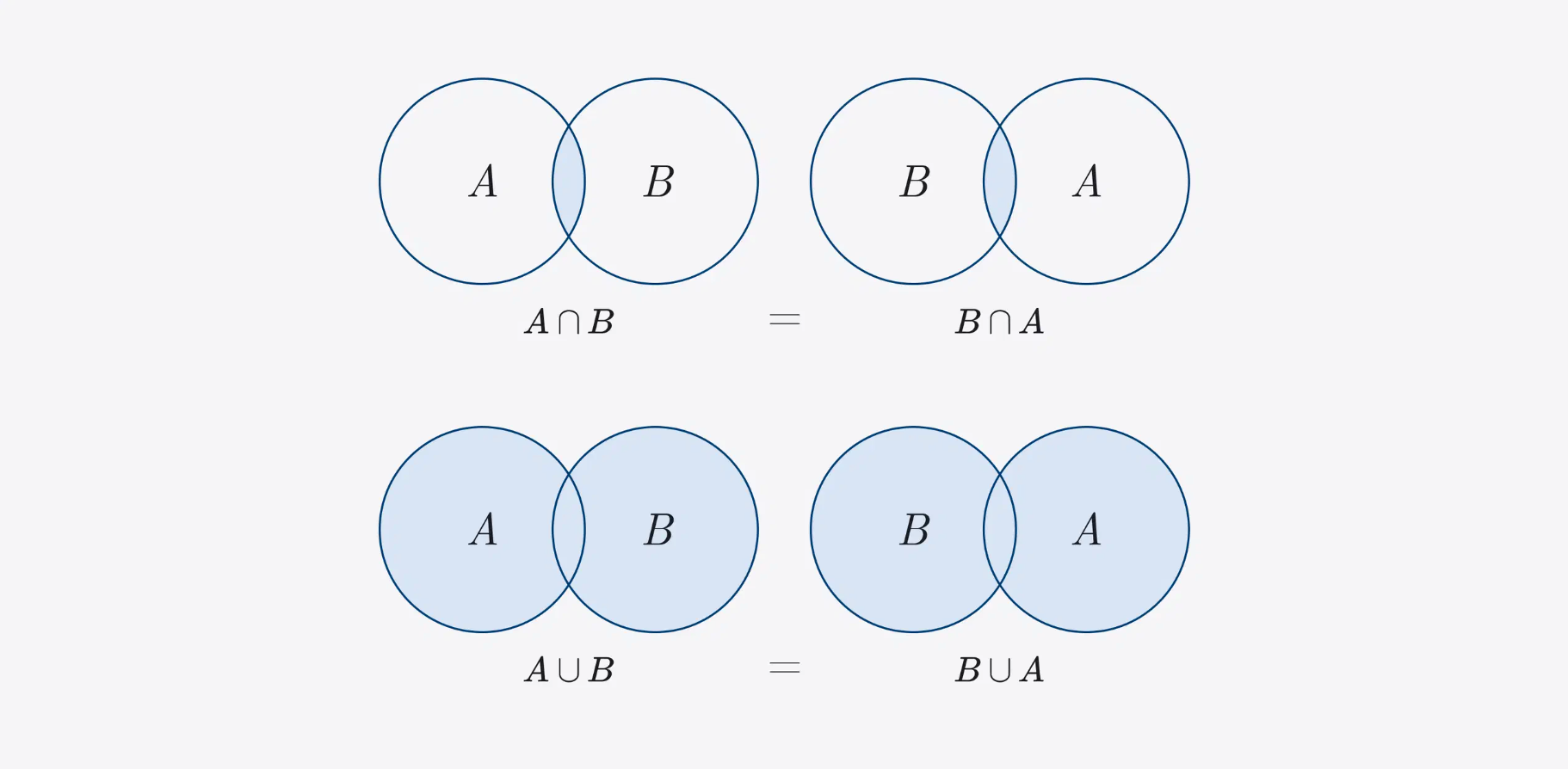
Commutativity property: regardless of the order of the sets, the elements of their intersection and union are unchanged.

A ∩ B = B ∩ A
A ∪ B = B ∪ A

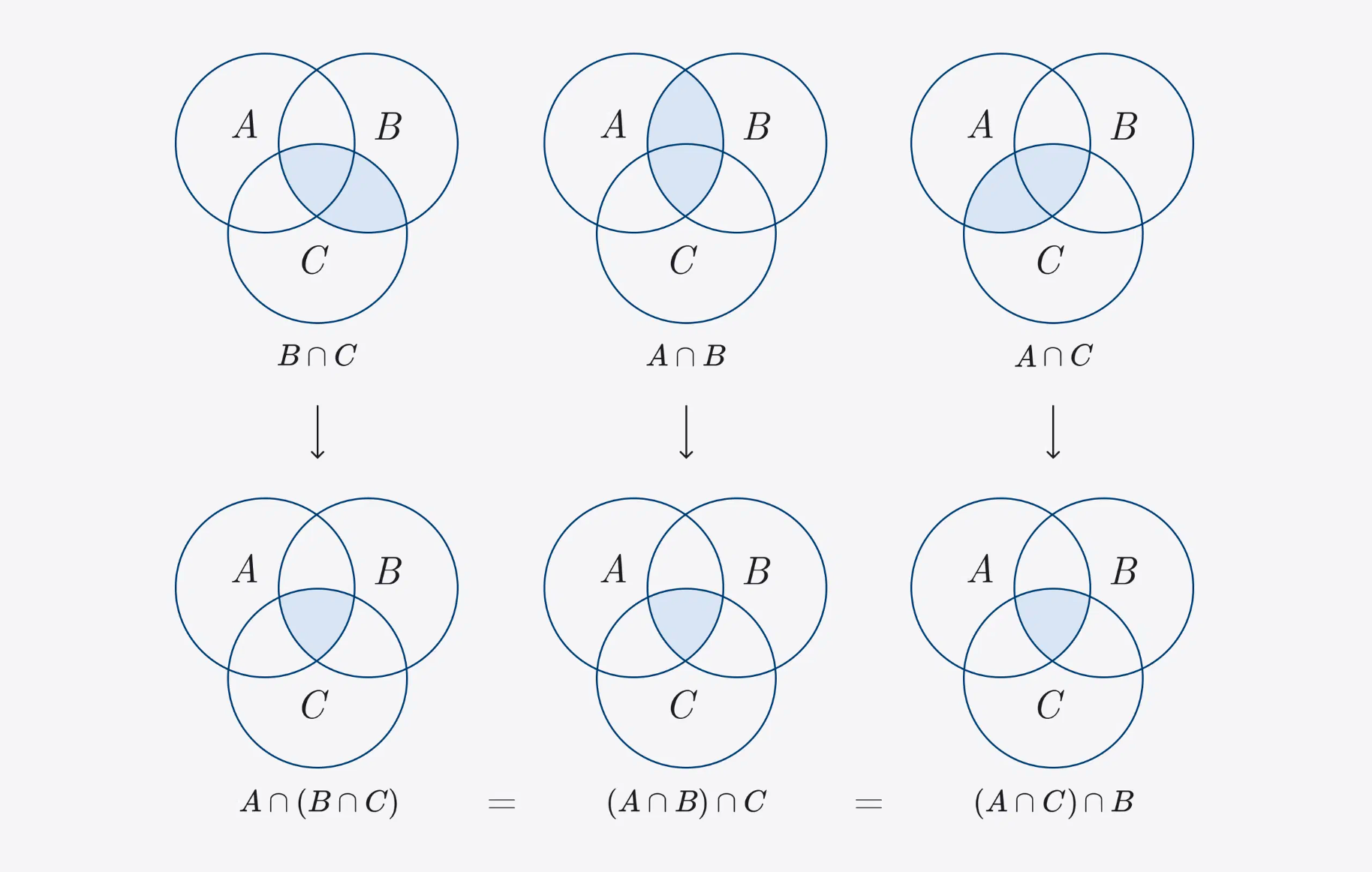
Associativity property: if there are three sets, you can find the intersection for two of them, and then add the third. Which two sets to start with doesn't matter. A ∩ (B ∩ C) = (A ∩ B) ∩ C

The associativity property can be illustrated using diagrams.

Similarly with union: A ∪ (B ∪ C)=(A ∪ B) ∪ C

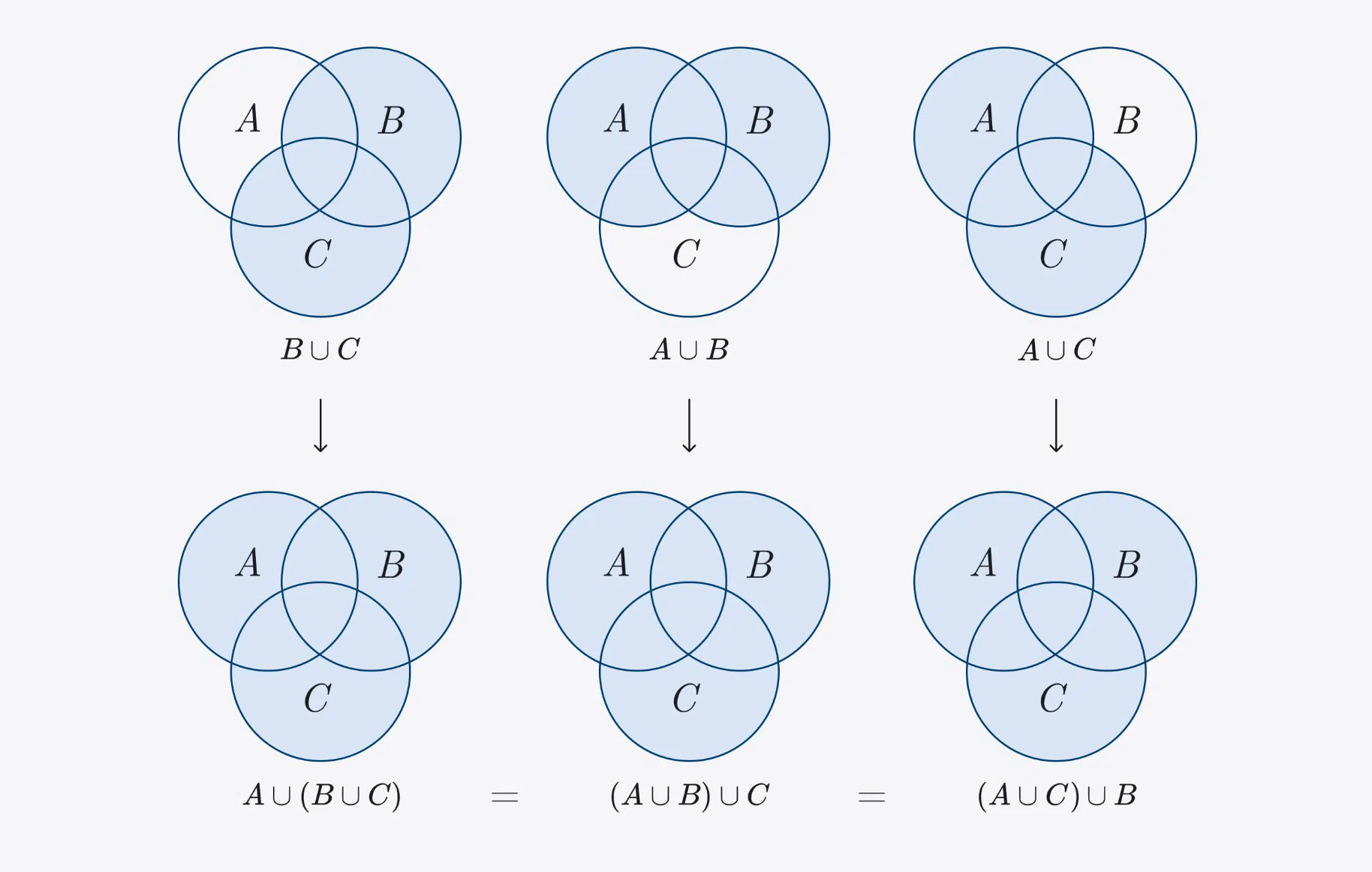
The same property in numerical form: a • (b • c) = (a • b) • c; a + (b + c) = (a + b) + c.

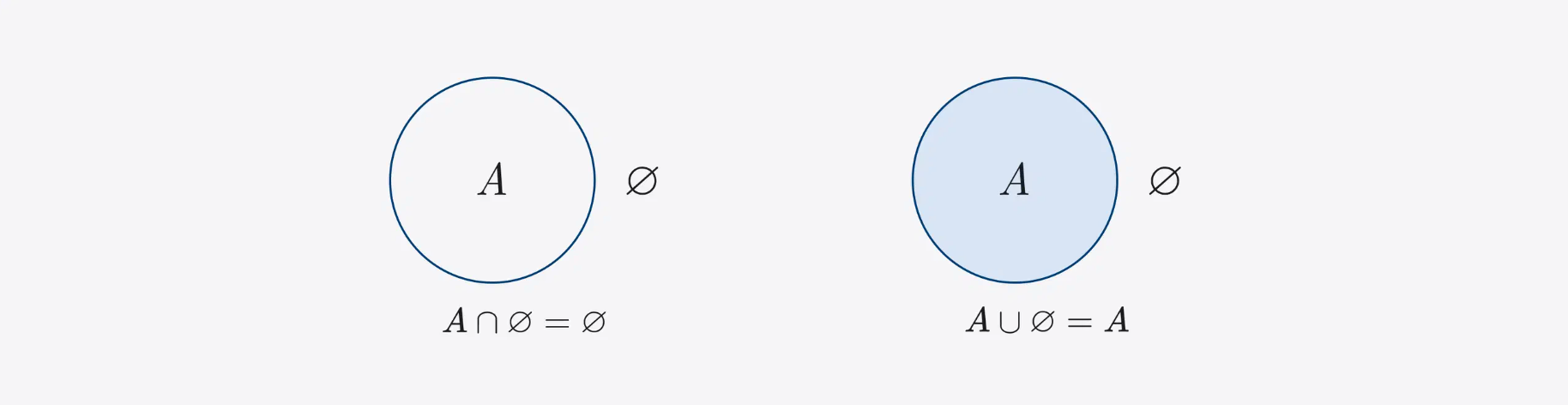
Intersection and union properties for an empty set: when any set intersects with an empty one, an empty set is obtained, when combined, the original set is obtained.

A ∩ ∅ = ∅ A ∪ ∅ = A

By analogy with operations with zero: a • 0 = 0; a + 0 = a

There are also properties that involve two operations at once.

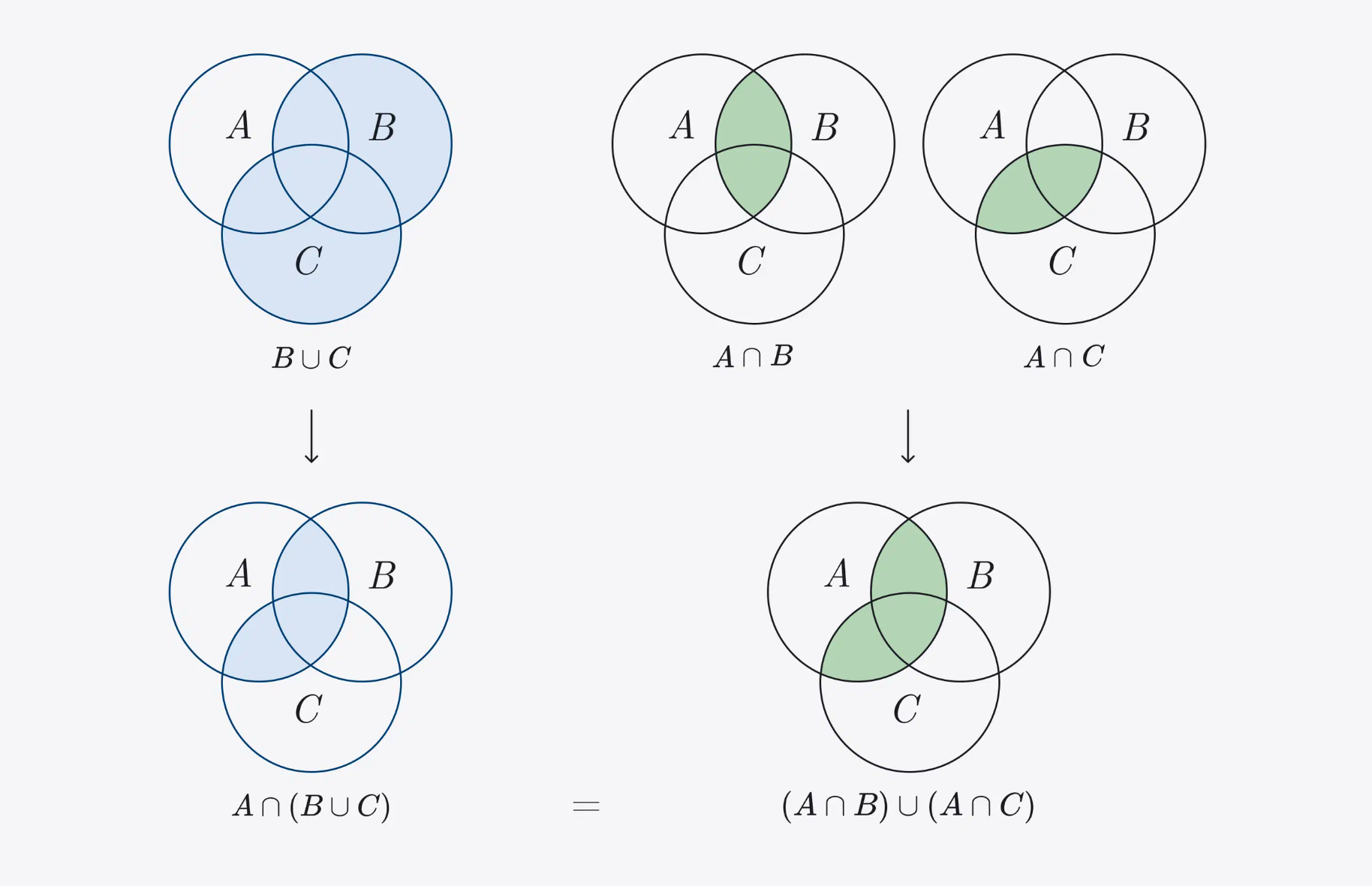
Distributivity of an intersection with respect to a union: to intersect A with union B ∪ C, we can intersect A ∩ B and A ∩ C, and then find the union of the resulting sets.

A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

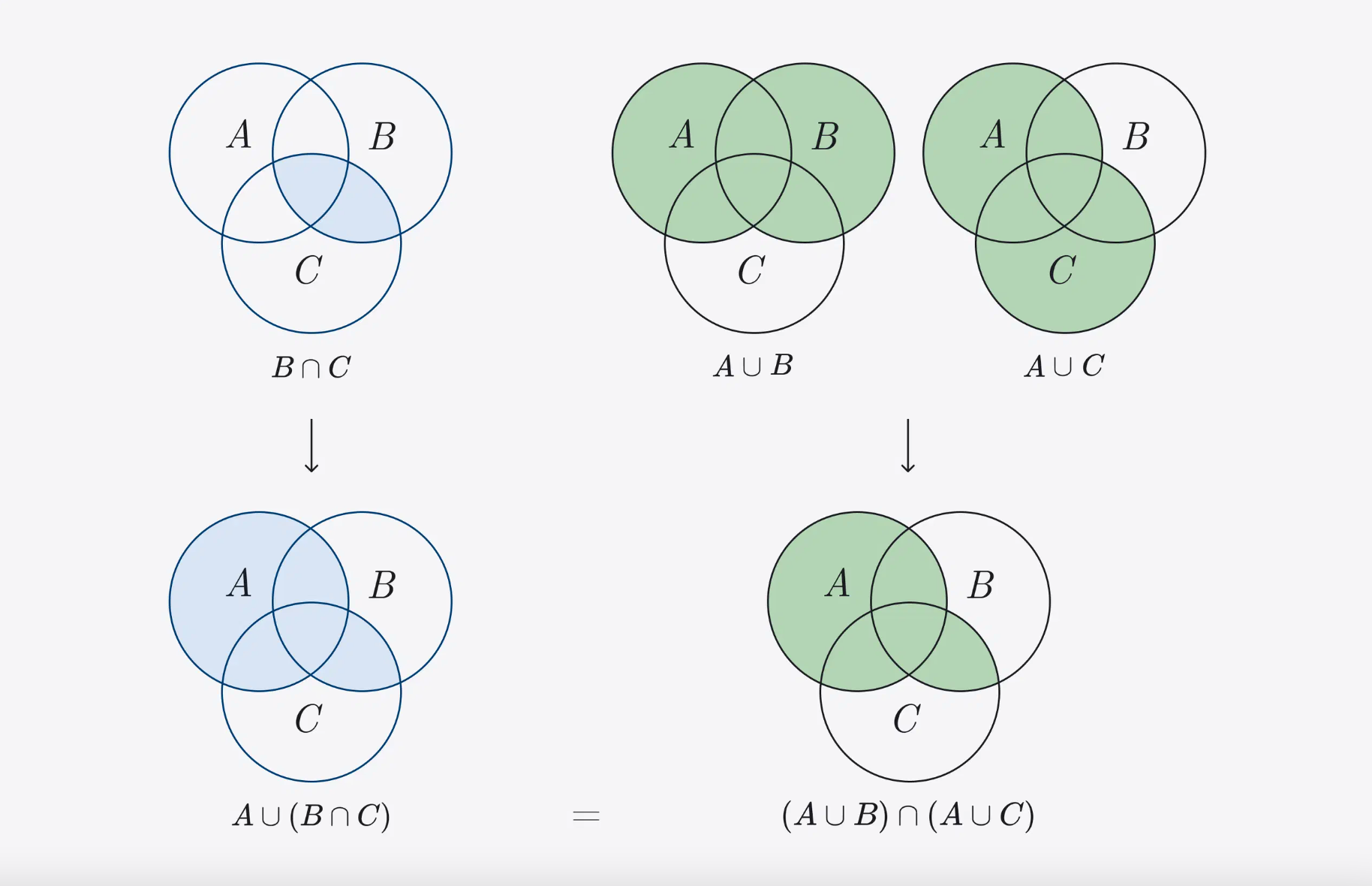
Distributivity of a union with respect to an intersection: to combine A with the intersection B ∩ C, you can combine A ∪ B and A ∪ C, and then find the intersection of these sets.

A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)

There is no longer an analogy with numbers. This property is unique and only works for sets. If we take the numbers a, b, c, then the expression a + (b • c) = (a + b) • (a + c) will be incorrect.

Example:

Let's find the elements of the set C ∪ (A ∩ B) from the diagram.

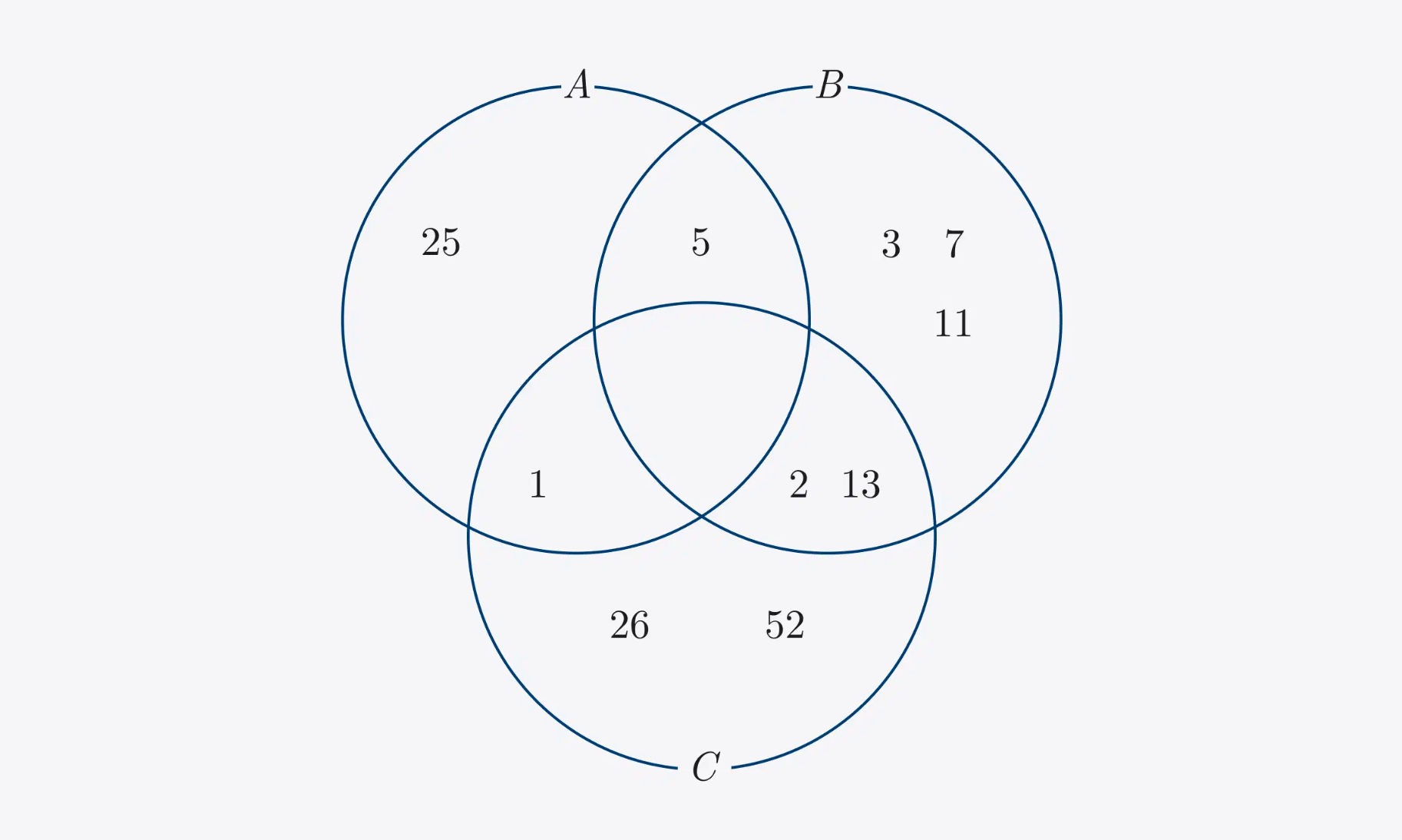
Solution: color the intersection A ∩ B and then add to it the set C.

Answer: the set C ∪ (A ∩ B) contains elements 1, 2, 5, 13, 26, 52.

‍

Union and intersection of multiple sets defined by a common property

If sets are given a common property, their intersection and union can also be found.

Example 1:

Let R be the set of numbers from the first hundred divisible by 30;
D is a set of even numbers from 85 to 100;
E is the set of two-digit numbers that are multiples of 10.

Now, let's find elements of the set (R ∪ D) ∩ E.

Solution: use the distributivity property: (R ∪ D) ∩ E = (R ∩ E) ∪ ( D ∩ E).

The intersection R ∩ E will contain numbers that are divisible by both 10 and 30. The number 30 is divisible by 10, so R ⊆ E, then R ∩ E=R.

In the intersection D ∩ E there will be two-digit even numbers from 85 to 100, which are divisible by 10. There is only one such number - 90. So, D ∩ E = {90}.

In the union R ∪ (D ∩ E) there will be multiples of 30 of the first hundred or the number 90. The number 90 is one of the multiples of 30, so R ∪ (D ∩ E) = R. Then, R = {30, 60, 90}.

‍

Example 2:

Let's take the same three sets and add one new one to them:

R be the set of numbers from the first hundred divisible by 30;
D is a set of even numbers from 85 to 100;
E is the set of two-digit numbers that are multiples of 10;
P is the set of prime numbers from 70 to 99.

Now let's find the elements of the set (R ∩ D) ∪ (E ∩ P).

Solution:‍

At the intersection R ∩ D there will be numbers divisible by30 that are between 85 and 100, which gives us the only number 90. So, R ∩ D = 90.

The intersection E ∩ P contains prime numbers from 70 to 99 that are divisible by 10. There are no such numbers, so E ∩ P = ∅.

When you combine any set with an empty set, you get the original set. (R ∩ D) ∪ ∅ =R ∩ D.

‍

I believe math can be intimidating with the severity of the wording and strange icons. In fact, it's just an alphabet that makes writing understandable to everyone who knows it. You just need to translate the properties into the language of examples, look for them around you and use math as a way to write it short and clear.

Your Cart